Вам понадобится
- Чертеж, карандаш, линейка.
Инструкция
1
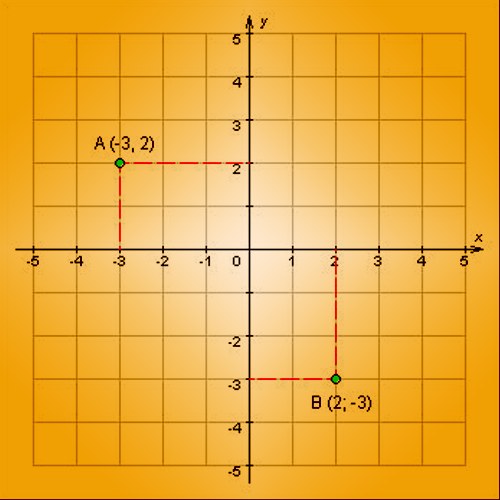
Если точка поставлена на чертеже, на котором есть и координатная сетка или хотя бы координатные оси с отмеченными на них единичными отрезками, для определения ее координат проведите пару вспомогательных отрезков. Один из них должен быть параллелен оси абсцисс, начинаться в точке, координаты которой определяются, а заканчиваться на оси ординат. Осью абсцисс обычно называют горизонтально расположенную ось с возрастающими слева направо значениями - ее обозначают буквой X. Ось ординат перпендикулярна ей и направлена от нижнего края листа к верхнему - ее обозначают буквой Y.
2
Измерьте длину проведенного горизонтального вспомогательного отрезка. Далеко не всегда деления системы координат совпадают с их длиной в сантиметрах, поэтому измерять длины следует в тех единицах, которые заданы единичными отрезками на координатных осях. Если точка расположена слева от вертикальной оси, измеренную величину надо считать отрицательной. Длина этого параллельного оси X отрезка с учетом знака определяет первую координату точки - абсциссу.
3
Проведите второй вспомогательный отрезок. Он должен быть параллелен оси ординат, начинаться в измеряемой точке и заканчиваться на оси абсцисс. Определите его длину по тем же правилам, что и в предыдущем шаге. Полученная величина даст вторую координату точки - ординату. Если точка расположена ниже горизонтальной оси, перед этой величиной нужно поставить минус. Получив пару значений, вы определите прямоугольные координаты точки в двухмерной декартовой системе. Например, если для некоторой точки A измеренные величины вдоль осей X и Y равны 5,7 и 8,1 соответственно, ее прямоугольные координаты можно записать так: A(5,7;8,1).
4
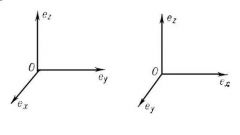
В трехмерной прямоугольной системе координат к абсциссам и ординатам добавляется третья ось - ось аппликат. Она обычно обозначается буквой Z, а в наборе чисел задающих положение точки в пространстве стоит на третьей позиции - например, A(5,7;8,1;1,1).