Инструкция
1
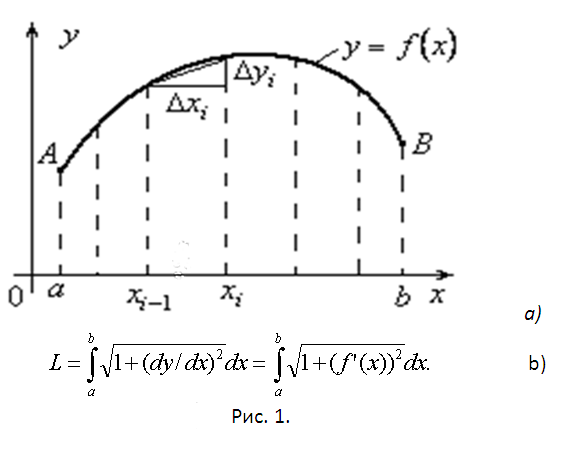
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.
2
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
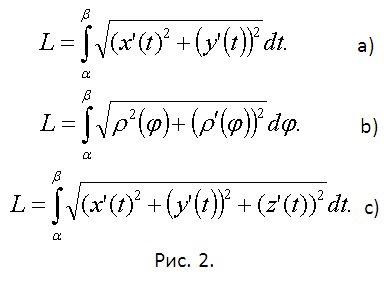
3
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
4
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Источники:
- Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для ВТУЗов. Т.1.-М.: Наука, 1972.-576 с.
- вычисление длины дуги с помощью определенного интеграла