Вам понадобится
- - формула поверхности площади шара;
- - формула объема шара;
- - навыки арифметического счета.
Инструкция
1
В повседневной жизни зачастую возникает необходимость вычислить площадь шаровой поверхности или его части, чтобы рассчитать, например, расход материала. Вычислив объем шара, вы можете через удельный вес рассчитать массу вещества, составляющего содержимое сферы. Для того чтобы найти площадь и объем шара, достаточно знать его радиус или диаметр. По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.
2
Например, диаметр футбольного мяча, согласно всем требованиям ФИФА, должен быть в пределах 21,8—22,2 см. Усредните для простоты счета до 22 см. Следовательно, радиус (R) будет равен (22:2) – 11 см. Ведь интересно узнать, какова площадь поверхности футбольного мяча?

3
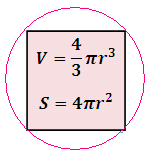
Возьмите формулу площади поверхности шара: Sшара = 4ттR2Подставьте в приведенную формулу значение радиуса футбольного мяча – 11 см.S = 4 x 3.14 x 11х11 .
4
После проведения несложных математических действий вы получаете результат: 1519.76. Таким образом, площадь поверхности футбольного мяча составляет 1 519.76 квадратных сантиметров.
5
Теперь рассчитайте объем мяча. Берите формулу расчета объема шара: V = 4/3ттR3Подставляйте опять же значение радиуса футбольного мяча – 11 см.V = 4/3 x 3.14 x 11 х 11 х 11.
6
После подсчетов, например, на калькуляторе вы получаете: 5576.89.Оказывается, объем воздуха в футбольном мяче составляет 5 576.89 кубических сантиметров.
Видео по теме
Обратите внимание
Интересно: объем шара с диаметром, превышающим в три раза диаметр другого шара, больше суммарного объема трех таких шаров в 9 раз.
Полезный совет
Чтобы развить у детей пристрастие к математическим вычислениям, предлагайте в качестве примеров для расчета окружающие предметы: мяч, арбуз, клубок бабушкиной пряжи. Это наглядно и потому интересно.