Вам понадобится
- Линейка, лист бумаги, ручка.
Инструкция
1
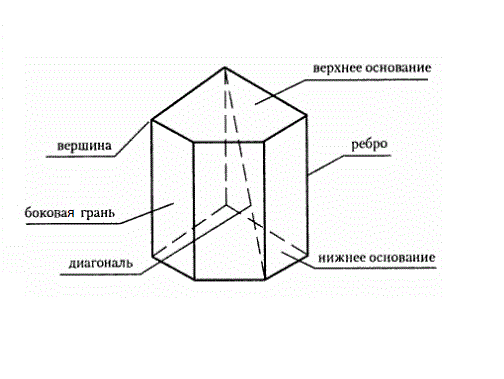
Разберитесь, что такое призма, и какой вид эта геометрическая фигура может иметь. Учтите, что слово «призма» переводится с латинского как «нечто отпиленное». Этот многогранник, всегда имеет два основания, которые расположены в параллельных плоскостях и являются равными многоугольниками. Они могут быть треугольными, четырехугольными, а также n-угольными.
2
Запомните, что количество остальных (боковых) граней зависит от вида основания. Если в основании треугольник, боковых граней соответственно окажется три, четырехугольник – четыре и так далее.
3
Имейте в виду, что ребра боковое ребро располагается под углом 90о к основанию, призма именуется прямой. В противном случае – наклонной. Если у прямой призмы в основании окажется правильный многоугольник, она превратится в правильную призму. Пример подобной геометрической фигуры – куб.
4
Чтобы вычислить периметр призмы, найдите периметры оснований и боковых граней призмы, и все размеры сложите друг с другом. Для этого измерьте при помощи линейки длины сторон (или ребра) каждой из граней. И посчитайте периметр каждого многоугольника.
5
Упростите свою задачу. Так как размер обоих оснований одинаков, померяйте длины ребер только у одного из них. Сложите размеры всех сторон и умножьте получившуюся сумму на два.
6
Если у оснований есть ребра равного размера, найдите количество одинаковых боковых граней. Измерьте длины сторон одной из этих граней, вычислите ее периметр. Умножьте получившееся значение на общее число одинаковых граней.
7
Отдельно посчитайте периметр каждой из тех боковых граней, которая ни разу не повторяется.
8
Сложите все посчитанные периметры – двух оснований, повторяющихся боковых граней, и тех боковых граней, которые не имеют аналога. Общая сумма будет равна периметру призмы.
Обратите внимание
Вычисление периметра не зависит от вида призмы. Он подсчитывается одинаково и для прямой, и для наклонной призмы.
Источники:
- Призмы