Как найти площадь параллелепипеда

Параллелепипед – объемная геометрическая фигура с тремя измерительными характеристиками: длиной, шириной и высотой. Все они участвуют в нахождении площади обеих поверхностей параллелепипеда: полной и боковой.

Инструкция

1. Параллелепипед – многогранник, построенный на основе параллелограмма. У него шесть граней, также являющихся этими двухмерными фигурами. В зависимости от того, как они расположены в пространстве, различают прямой и наклонный параллелепипед. Эта разница выражается в равенстве угла между основанием и боковым ребром 90°.
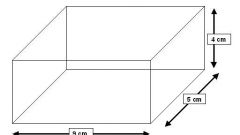
2. По тому, к какому частному случаю параллелограмма относится основание, можно выделить прямоугольный параллелепипед и наиболее распространенную его разновидность – куб. Эти формы наиболее часто встречаются в повседневной жизни и носят название стандартных. Они присущи бытовой технике, предметам мебели, электронным приборам и др., а также самим человеческим жилищам, размеры которых имеют большое значение для обитателей и риелторов.
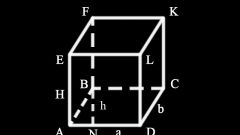
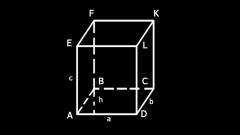
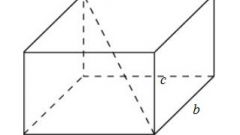
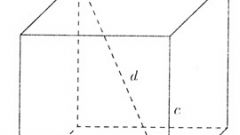
3. Обычно считают характеристика представляет собой совокупность площадей его граней, вторая – та же величина плюс площади обоих оснований, т.е. сумма всех двухмерных фигур, из которых состоит параллелепипед. Следующие формулы носят название основных наряду с объемом:Sб = Р•h, где Р – пeримeтр основания, h – высота;Sп = Sб + 2•S, где So – площадь основания.

Для частных случаев, куба и фигуры с прямоугольными основаниями, формулы упрощаются. Теперь уже не нужно определять высоту, которая равна длине вертикального ребра, а площадь и периметр найти гораздо легче благодаря наличию прямых углов, в их определении участвуют только длина и ширина. Итак, для прямоугольного параллелепипеда:Sб = 2•с•(a + b), где 2•(а + b) – удвоенная сумма сторон основания (периметр), с – длина бокового ребра;Sп = Sб + 2•а•b = 2•а•с + 2•b•с + 2•a•b = 2•(а•с + b•с + а•b).

У куба все ребра имеют одинаковую длину, следовательно:Sб = 4•а•а = 4•а²;Sп = Sб + 2•а² = 6•а².