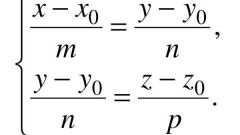Инструкция
1
Первый случай. Дана прямая у=kx+b на плоскости. Требуется найти уравнение перпендикулярной ей прямой, проходящей через точку M(m, n). Уравнение этой прямой ищите в виде y=cx+d. Используйте геометрический смысл коэффициента k. Это тангенс угла наклона α прямой к оси абсцисс k=tgα. Тогда с=tg(α+π/2)=-ctgα=-1/tgα=-1/k. На данный момент найдено уравнение перпендикулярной прямой в виде y=-(1/k)x+d, в котором осталось уточнить d. Для этого используйте координаты заданной точки М(m, n). Запишите уравнение n=-(1/k)m+d, из которого d=n-(1/k)m. Теперь можно дать ответ y=-(1/k)x+n-(1/k)m. Существуют и другие виды уравнений плоской прямой. Поэтому есть и другие способы решений. Правда, все они легко преобразуются друг в друга.
2
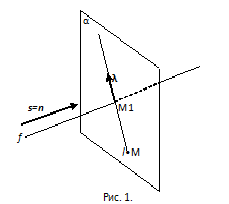
Пространственный случай. Пусть известная прямая f задана каноническими уравнениями (если это не так, приведите их к каноническому виду). f: (x-x0)/m=(y-y0)/n=(z-z0)/p, где М0(x0, y0, z0) – произвольная точка этой прямой, а s={m,n,p} – ее направляющий вектор. Заданная точка М(a,b,c). Сначала найдите плоскость α, перпендикулярную прямой f, содержащую М. Для этого используйте одну из форм общего уравнения прямой A(x-a)+B(y-b)+C(z-c)=0. Ее направляющий вектор n={A,B,C} совпадает с вектором s (см. рис. 1). Поэтому n={m,n,p} и уравнение α: m(x-a)+n(y-b)+p(z-c)=0.
3
Теперь найдите точку М1(x1,y1,z1) пересечения плоскости α и прямой f путем решения системы уравнений (x-x0)/m=(y-y0)/n=(z-z0)/p и m(x-a)+n(y-b)+p(z-c)=0. В процессе решения возникнет одинаковая для всех искомых координат величина u= [m(x0-a)+n(y0-b)+p(z0-c)]/(m^2+n^2+p^2). Тогда решение x1=x0-mu, y1=y0-nu, z1=z0-pu.
4
На этом шаге поиска перпендикулярной прямой ℓ, найдите ее направляющий вектор g=M1M={x1-a,y1-b,z1-c}={х0-mu-a,y0-nu-b,z0-pu-c}. Положите координаты этого вектора m1=х0-mu-a, n1=y0-nu-b, p1=z0-pu-c и запишите ответ ℓ: (x-a)/(х0-mu-a)=(y-b)/(y0-nu-b)=(z-c)/(z0-pu-c).