Инструкция
1
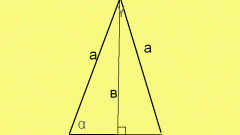
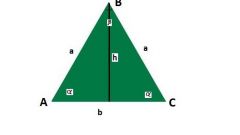
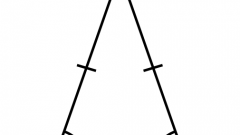
Высоту (Hc), проведенную к основанию равнобедренного треугольника, можно рассчитать, зная длины этого основания (c) и боковой стороны (a). Для этого можно использовать теорему Пифагора, так как высота, боковая сторона и половина основания образуют прямоугольный треугольник. Высота и половина основания в нем являются катетами, поэтому для решения задачи извлеките корень из разности между возведенной в квадрат длиной боковой стороны и четвертью квадрата длины основания: Hс = √(a²-¼*c²).
2
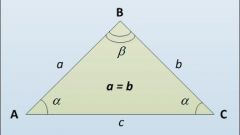
Эту же высоту (Hc) можно вычислить и по длине любой из сторон, если в условиях приведена величина хотя бы одного угла. Если это угол при основании треугольника (α) а известная длина определяет величину боковой стороны (a), для получения результате перемножьте длину известной стороны и синус известного угла: Hс = a*sin(α). Эта формула вытекает из теоремы синусов.
3
Если известна длина основания (с) и величина прилегающего к нему угла (α), для вычисления высоты (Hc), половину длины основания умножьте на синус известного угла и разделите на синус разницы между 90° и величиной того же угла: Hс = ½*c*sin(α)/sin(90°-α).
4
При известных размерах основания (с) и противолежащего ему угла (γ) для вычисления высоты (Hc) умножайте половину длины известной стороны на синус разницы между 90° и половиной известного угла, а результат делите на синус половины того же угла: Hс = ½*c*sin(90°-γ/2)/sin(γ/2). Эта формула, как и две предыдущие, вытекает из теоремы синусов в сочетании с теоремой о сумме углов в треугольнике.
5
Длину высоты, проведенной к одной из боковых сторон (Ha) можно вычислить, например, зная длину этой стороны (a) и площадь равнобедренного треугольника (S). Чтобы это сделать, найдите удвоенную величину соотношения между площадью и длиной известной стороны: Ha = 2*S/a.