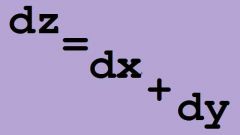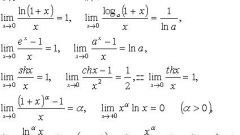Как вычислить пределы функций, не пользуясь средствами дифференциального исчисления

Вычисление пределов с применением способов дифференциального исчисления основывается на правиле Лопиталя. При этом известны примеры, когда это правило не применимо. Поэтому остается актуальной и задача вычисления пределов обычными способами.

Инструкция

1. Непосредственное вычисление пределов связано, в первую очередь, с пределами рациональных дробей Qm(x)/Rn(x), где Q и R многочлены. Если вычисляется предел при х →a (a – число), то может возникнуть неопределенность, например [0/0]. Для ее устранения просто поделите числитель и знаменатель на (х-а). Операцию повторяйте до тех пор, пока неопределенность не пропадет. Деление многочленов осуществляется практически так же, как и деление чисел. Оно основано на том, что деление и умножение – обратные операции. Пример приведен на рис. 1.
   
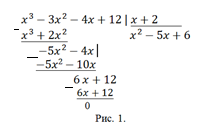
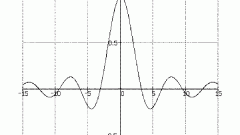
2. Применение первого замечательного предела. Формула для первого замечательного предела приведена на рис. 2а. Для его применения приведите выражение вашего примера к соответствующему виду. Это всегда можно сделать чисто алгебраически или заменой переменной. Главное - не забывайте, что если синус берется от kx, то и знаменатель тоже kx. Пример рассмотрен на рис. 2e.Кроме того, если учесть, что tgx=sinx/cosx, cos0=1, то, как следствие, появляется формула (см. рис. 2b). arcsin(sinx)=x и arctg(tgx)=x. Поэтому имеются еще два следствия (рис 2с. и 2d). Возник еще достаточно широкий набор способов вычисления пределов.
   
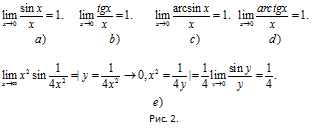
3. Применение второго замечательно предела (см. рис. 3а)Пределы такого типа используются для устранения неопределенностей типа [1^∞]. Для решения соответствующих задач просто преобразуйте условие до структуры, соответствующей виду предела. Помните, что при возведении в степень выражения, уже находящегося в какой-либо степени, их показатели перемножаются. Соответствующий пример приведен на рис. 2е.Примените подстановку α=1/х и получите следствие из второго замечательного предела (рис. 2b). Прологарифмировав по основанию а обе части этого следствия, придете ко второму следствию, в том числе и при а=е (см. рис. 2с). Сделаете замену а^x-1=y. Тогда x=log(a)(1+y). При стремлении х к нулю, у также стремится к нулю. Поэтому возникает и третье следствие (см. рис. 2d).
   
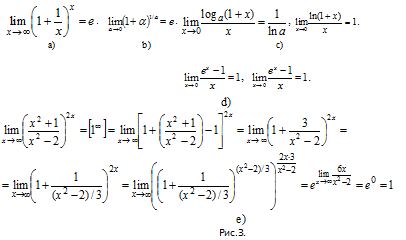
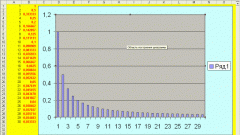
4. Применение эквивалентных бесконечно малых.Бесконечно малые функции эквивалентны при х →а, если предел их отношения α(х)/γ(х) равен единице. При вычислении пределов с помощью таких бесконечно малых просто запишите γ(x)=α(x)+o(α(x)). o(α(x)) – это бесконечно малая более высокого порядка малости, чем α(x). Для нее lim(x→a)o(α(x))/α(x)=0. Для выяснения эквивалентности используйте те же замечательные пределы. Метод позволяет существенно упростить процесс нахождения пределов, сделав его более прозрачным.