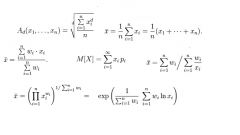Инструкция
1
Вычисление математического ожидания случайной величины является одним из основных этапов оценки степени ее отклонения от истинного значения. Во время построения вероятностной модели измеряемого параметра эта числовая характеристика показывает, насколько далеко от истины ее среднее ожидаемое значение.
2
Чтобы вычислить математическое ожидание, необходимо рассмотреть выборку значений функции распределения случайной величины. Элементы этой функции представляют собой вероятности, с которыми величина окажется равной тому или иному значению из множества X.
3
Очевидно, что выборка значений (результатов серии измерений) анализируемого параметра является числовым рядом. Следовательно, чтобы найти его среднее значение, необходимо определить интегральную сумму этого ряда. Это приводит к операции интегрирования и использованию формулы Лебега-Стильтьеса:M = ∫xdF(x).
4
Разделяют понятия математического ожидания дискретной и целой величины. Первое вытекает из интеграла, приведенного выше, и представляет собой суммирование попарных произведений соответствующих друг другу элементов двух множеств: выборки значений изучаемого параметра и массива вероятностей, с которыми эти значения может принять случайная величина. Тогда формула выглядит следующим образом:М = Σxi•pi, где i – индекс суммы, принадлежащий интервалу от 1 до бесконечности.
5
Математическое ожидание целой величины равно первой производной функции последовательности. При этом очевидно, что целая величина имеет распределение вероятностей, равное Σpi = 1, поэтому в продифференцированную функцию подставляется значение, равное x=1. Тогда формула принимает вид:M = P’(1) = Σk•p_k.
6
Необходимо помнить, что производящая функция последовательности сама по себе является числовым рядом, поэтому от его сходимости зависит, существует ли конечное значение математического ожидания. Если же ряд расходится, то эта характеристика случайной величины равна бесконечности, т.е. не определена.