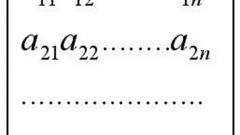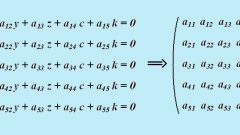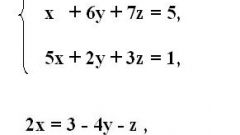Инструкция
1
Определитель квадратной матрицы – это число, которое используется в различных расчетах. Он незаменим при нахождении обратной матрицы, миноров, алгебраических дополнений, операции деления матриц, но чаще всего необходимость перехода к определителю возникает при решении систем линейных уравнений.
2
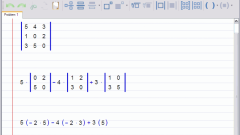
Чтобы вычислить определитель второго порядка, нужно воспользоваться формулой разложения по первой строке. Он равен разности попарных произведений элементов матрицы, расположенных на главной и побочной диагонали соответственно:∆ = a11•a22 – a12•a21.
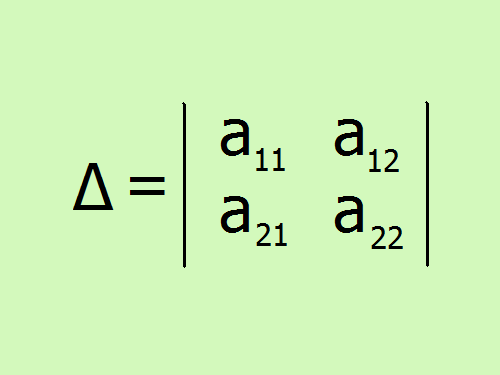
Как вычислить определитель <b>второго</b> <em>порядка</em>
3
Матрица второго порядка представляет собой совокупность четырех элементов, расположенных на двух строках и столбцах. Эти числа соответствуют коэффициентам системы уравнений с двумя неизвестными, которые применяются при рассмотрении множества прикладных задач, например, экономических.
4
Переход к компактным матричным вычислениям помогает быстро определить две вещи: во-первых, имеет ли эта система решение, во-вторых, найти его. Достаточным условием существования решения является неравенство определителя нулю. Это связано с тем, что при вычислении неизвестных составляющих уравнений это число стоит в знаменателе.
5
Итак, пусть есть система из двух уравнений с двумя переменными x и y. Каждое уравнение состоит из пары коэффициентов и свободного члена. Тогда составляется три матрицы второго порядка: элементы первой – коэффициенты при x и y, вторая содержит свободные члены вместо коэффициентов при x, а третья – вместо числовых множителей при переменной y.
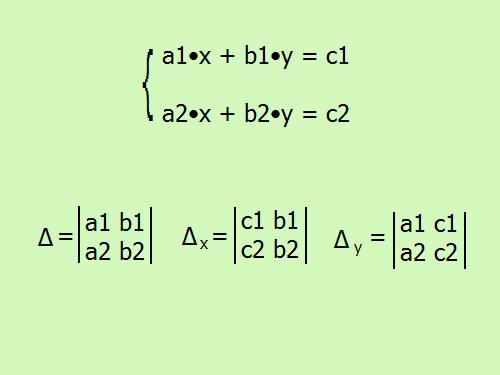
Как вычислить определитель <b>второго</b> <em>порядка</em>
6
Тогда значения неизвестных можно вычислить следующим образом:x = ∆x/∆; y = ∆y/∆.
7
После выражения через соответствующие элементы матриц, получается:∆ = a1•b2 – b2•a1; ∆x = c1•b2 – b1•c2 → x = (c1•b2 – b1•c2)/(a1•b2 – b2•a1);∆y = a1•c2 – c1•a2 → y = (a1•c2 – c1•a2)/(a1•b2 – b2•a1).