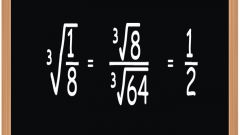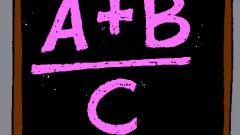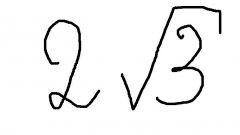Инструкция
1
Прежде чем избавиться от иррациональности дроби в знаменателе, следует определить ее тип, и в зависимости от этого продолжать решение. И хотя любая иррациональность следует из простого присутствия корней, различные их комбинации и степени предполагают разные алгоритмы.
2
Квадратный корень в знаменателе, выражение вида a/√bВведите дополнительный множитель, равный √b. Чтобы дробь не изменилась, умножать нужно и числитель, и знаменатель:a/√b → (a•√b)/b.Пример 1: 10/√3 → (10•√3)/3.
3
Наличие под чертой дроби корня дробной степени вида m/n, причем n>mЭто выражение выглядит следующим образом:a/√(b^m/n).
4
Избавьтесь от подобной иррациональности также путем ввода множителя, на этот раз более сложного: b^(n-m)/n, т.е. из показателя степени самого корня нужно вычесть степень выражения под его знаком. Тогда в знаменателе останется только первая степень:a/(b^m/n) → a•√(b^(n-m)/n)/b.Пример 2: 5/(4^3/5) → 5•√(4^2/5)/4 = 5•√(16^1/5)/4.
5
Сумма квадратных корнейУмножьте обе составляющих дроби на аналогичную разность. Тогда из иррационального сложения корней знаменатель преобразуется в разность выражений/чисел под знаком корня:a/(√b + √c) → a•(√b - √c)/(b - c).Пример 3: 9/(√13 + √23) → 9•(√13 - √23)/(13 - 23) = 9•(√23 - √13)/10.
6
Сумма/разность кубических корнейВыберите в качестве дополнительного множителя неполный квадрат разности, если в знаменателе стоит сумма, и соответственно неполный квадрат суммы для разности корней:a/(∛b ± ∛c) → a•(∛b² ∓ ∛(b•c) + ∛c²)/ ((∛b ± ∛c)• ∛b² ∓ ∛(b•c) + ∛c²) →a•(∛b² ∓ ∛(b•c) + ∛c²)/(b ± c).Пример 4: 7/(∛5 + ∛4) → 7•(∛25- ∛20 + ∛16)/9.
7
Если в задаче присутствует и квадратный и кубический корень, тогда разделите решение на два этапа: последовательно выведите из знаменателя квадратный корень, а затем кубический. Делается это по уже известным вам методам: в первом действии нужно выбрать множитель разности/суммы корней, во втором – неполный квадрат суммы/разности.