Инструкция
1
Для того чтобы дальнейшее было понятнее, начните с плоского случая. Конечно слово «вывернем» следует брать в кавычках. Рассмотрите окружность x^2+y^2=R^2. Примените криволинейные координаты. Для этого сделайте замены переменных u=R/x, v=R/y, соответственно обратное преобразование x=R/u, y=R/v. Подставьте это в уравнение окружности и получите [(1/u)^2+(1/v)^2]*R^2=R^2 или (1/u)^2+(1/v)^2=1. Далее (u^2+v^2)/(u^2)(v^2)=1, или u^2+v^2=(u^2)(v^2). Графики таких функций не укладываются в рамки кривых второго порядка (здесь четвертый порядок).
2
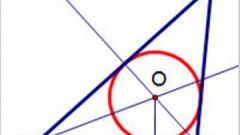
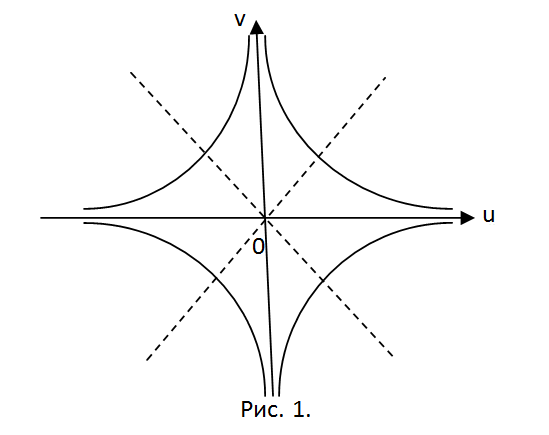
Для того чтобы стал ясен вид кривой в координатах u0v, рассматриваемых как декартовы, перейдите к полярным координатам ρ=ρ(φ). При этом u=ρcosφ, v=ρsinφ. Тогда (ρcosφ)^2+(ρsinφ)^2=[(ρcosφ)^2][(ρsinφ)^2]. (ρ^2)[(cosφ)^2+(sinφ)^2]=(ρ^4)[(cosφ)^2][(sinφ)^2], 1=(ρ^2)[(cosφ)(sinφ)]^2. Примените формулу синуса двойного угла и получите ρ^2=4/(sin2φ)^2 или ρ=2/|(sin2φ)|. Ветви этой кривой очень похожи на ветви гиперболы (см. рис. 1).
3
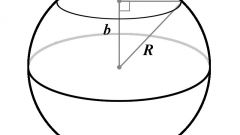
Теперь вам следует перейти к сфере x^2+y^2+z^2=R^2. По аналогии с окружностью сделайте замены u=R/x, v=R/y, w=R/z. Тогда x=R/u, y=R/v, z=R/w. Далее получите [(1/u)^2+(1/v)^2+(1/w)^2]*R^2=R^2, (1/u)^2+(1/v)^2+(1/w)^2=1 или (u^2)(v^2)+(u^2)(w^2)+(v^2)(w^2)=(u^2)(v^2)(w^2). К сферическим координатам в пределах 0uvw, рассматриваемых как декартовы, переходить не следует, так как это не внесет облегчения в поиске эскиза полученной поверхности.
4
Тем не менее, этот эскиз уже обозначился из предварительных данных плоского случая. Кроме того, очевидно, что это - поверхность, состоящая из отдельных фрагментов, и что координатных плоскостей u=0, v=0, w=0 эти фрагменты не пересекают. Они могут приближаться к ним асимптотически. В целом фигура состоит из восьми фрагментов похожих на гиперболоиды. Если дать им название «условный гиперболоид», то можно говорить о четырех парах двуполостных условных гиперболоидов, осью симметрии которых являются прямые с направляющими косинусами {1/√3, 1/√3, 1/√3}, {-1/√3, 1/√3, 1/√3}, {1/√3, -1/√3, 1/√3}, {-1/√3, -1/√3, 1/√3}. Иллюстрацию привести достаточно затруднительно. Тем не менее, приведенное описание можно считать достаточно полным.