Инструкция
1
Определите признаки возрастания или убывания заданной функции. Для линейной функции вида f(x) = k*а+b имеет значение знак коэффициента при аргументе х. Если k>0, функция возрастает, при k
2
Найдите значения функции в заданном интервале [n, m]. Для этого подставьте граничные значения в качестве аргумента х в выражение функции. Произведите вычисления f (х), запишите результаты. Обычно поиск значений выполняется для построения графика функции. Однако двух пограничных точек для этого недостаточно. На указанном интервале задайте шаг в 1 или 2 единицы, в зависимости от промежутка, прибавляйте значение х на величину шага и каждый раз высчитывайте соответствующее значение функции. Оформите результаты в табличном виде, где одной строкой будет аргумент х, второй – значения функции.
3
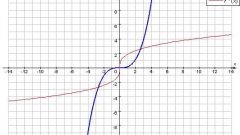
Постройте график функции на координатной плоскости ОХУ. Здесь горизонтальная ОХ является осью абсцисс, на которой отображаются все аргументы, вертикальная ОУ – ось ординат со значениями функции. Отложите на осях все полученные данные х и у (f(x)). Поставьте точки функции на пересечении соответствующих значений х и у. Плавной линией последовательно соедините точки и подпишите рядом с графиком выражение функции.
4
дифференциал данной функции f'(x) равен нулю или не существует.
5
Дифференцируйте заданную функцию. Приравняйте полученное выражение к нулю и найдите аргументы, при которых равенство истинно. Подставьте поочередно каждое из полученных значений х в уравнение дифференцированной функции, вычислите выражение и определите его знак. Если производная f'(x) меняет знак с плюса на минус, найденная точка является точкой максимума, при обратном результате – определена точка минимума. Найденные аргументы хmin и xmax подставьте в первоначальную функцию f(x) и вычислите ее значения в обоих случаях. Вы найдете соответствующие экстремумы функции.
Видео по теме