Инструкция
1
Радиус-вектор принято записывать следующим образом: r=r(М)=x∙i+y∙j+z∙k. Здесь (x, y, z) – декартовы координаты вектора. Не трудно представить ситуацию, когда вектор может изменяться в зависимости от какого-либо скалярного параметра, например, времени t. В этом случае вектор можно описывать как функцию трех аргументов, заданную параметрическими уравнениями x=x(t), y=y(t), z=z(t), что соответствует r=r(t)=x(t)∙i+y(t)∙j+z(t)∙k. При этом линия, которую по мере изменения параметра t описывает в пространстве конец радиус-вектора называется годографом вектора, а само соотношение r=r(t) называют вектор-функцией (векторной функцией скалярного аргумента).
2
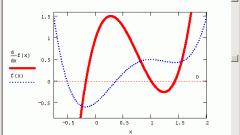
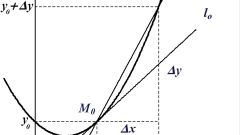
Итак, вектор-функция – это вектор, зависящий от параметра. Производную вектор-функции (как и любой функции, представляемой в виде суммы) можно записать в следующей форме: r’=dr/dt=r’(t)= x’(t)∙i+y’(t)∙j+z’(t)∙k. (1)Производная каждой из входящих в (1) функций определяется традиционно. Аналогичным образом обстоит дело и с r=r(t), где приращение ∆r также вектор (см. рис. 1).
3
В силу (1) можно прийти к выводу, что правила дифференцирования вектор-функции повторяют правила дифференцирования обычных функций. Так производная суммы (разности) – есть сумма (разность) производных. При вычислении производной вектора на число, это число можно выносить за знак производной. Для скалярного и векторного произведения сохраняется правило вычисления производной произведения функций. Для векторного произведения [r(t),g(t)]’= [r’(t),g(t)]+[r(t)g’(t)]. Остается еще одно понятие – произведения скалярной функции на векторную (здесь правило дифференцирования произведения функций сохраняется).
4
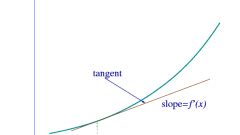
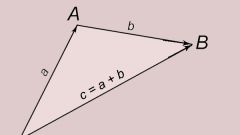
Особый интерес представляет собой вектор-функция длины дуги s, по которой перемещается конец вектора, отсчитываемой от некоторой начальной точки Мо. Это r=r(s)=u(s)∙i+v(s)∙j+w(s)∙k (см. рис. 2).С помощью рис. 2 постарайтесь выяснить геометрический смысл производной dr/ds.
5
Отрезок АВ, на котором лежит ∆r, является хордой дуги. При этом ее длина равна ∆s. Очевидно, что отношение длины дуги к длине хорды стремится к единице при ∆r, стремящимся к нулю. ∆r=r∙(s + ∆s)-r(s), |∆r |=|AB|. Поэтому |∆r/∆s| и в пределе (при ∆s стремящимся к нулю) равно единице. Получаемая при этом производная направлена по касательной к кривой dr/ds=&sigma – единичный вектор. Следовательно, можно записать и вторую производную (d^2)r/(ds)^2=(d/ds)[dr/ds]=d&sigma/ds.
Видео по теме