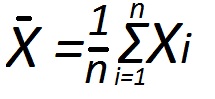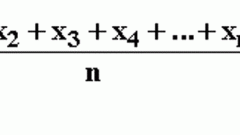Вам понадобится
- калькулятор.
Инструкция
1
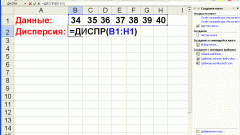
Дисперсия в математической статистике и теории вероятностей определяется как мера рассеивания (отклонения от среднего). Чем меньше значение этого показателя, тем однороднее совокупность и тем в более близком диапазоне будет находиться средняя величина.
2
В эконометрических расчетах, как правило, используют общую, межгрупповую и внутригрупповую дисперсии. При этом первая характеризует, как изменяется признак совокупности под влиянием всех факторов, действующих на нее. Ее можно рассчитать по формуле:
σ^2общ = (сумма(х-хср)*f)/сумма f, где
хср – средняя арифметическая общая для всей совокупности.
σ^2общ = (сумма(х-хср)*f)/сумма f, где
хср – средняя арифметическая общая для всей совокупности.
3
Межгрупповая дисперсия показывает, насколько отклоняется средняя каждой группы от общей для всех групп. Она отражает влияние фактора, положенного в основание группировки. Ее можно найти следующим образом:
σ^2м = (сумма(хiср-хср)*ni)/сумма ni, где
хiср – среднее значение признака по отдельной группе;
ni – количество единиц в группе;
хср – средняя величина, характерная для всего числа групп.
σ^2м = (сумма(хiср-хср)*ni)/сумма ni, где
хiср – среднее значение признака по отдельной группе;
ni – количество единиц в группе;
хср – средняя величина, характерная для всего числа групп.
4
Внутригрупповая (остаточная) дисперсия характеризует колебание признака внутри каждой группы. Она говорит о случайной вариации и не зависит от признака, положенного в основу группировки. Для ее расчета сначала необходимо найти дисперсии по отдельным группам:
σ^2вi = (сумма(х-хiср)*ni)/сумма ni, где
хiср – средняя для каждой группы.
А затем среднюю для всех групп по формуле:
σ^2iср = (сумма(σ^2вi*ni)/сумма ni.
σ^2вi = (сумма(х-хiср)*ni)/сумма ni, где
хiср – средняя для каждой группы.
А затем среднюю для всех групп по формуле:
σ^2iср = (сумма(σ^2вi*ni)/сумма ni.
5
Все они связаны между собой: общая дисперсия равна сумме межгрупповой и внутригрупповой средней. Это соотношение отражает правило сложения дисперсий. Его можно представить следующим образом:
σ^2общ = σ^2м+ σ^2iср
σ^2общ = σ^2м+ σ^2iср
6
С помощью этого правила можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки. Чем выше доля межгрупповой дисперсии в общей, тем сильнее влияние этого фактора.
Видео по теме
Источники:
- остаточная дисперсия