Как построить ортогональную проекцию

Ортогональную, или прямоугольную, проекцию (от лат. proectio − «бросание вперед») можно физически представить как тень, отбрасываемую фигурой. При конструировании зданий и других объектов также используется проекционное изображение.

Инструкция

1. Чтобы получить проекцию точки на ось, постройте перпендикуляр к оси из этой точки. Основание перпендикуляра (точка, в которой перпендикуляр пересекает ось проекции) и будет, по определению, искомой величиной. Если точка на плоскости имеет координаты (x,y), то ее проекция на ось Ox будет иметь координаты (x,0), на ось Oy − (0,y).
2. Пусть теперь на плоскости задан отрезок. Чтобы найти его проекцию на координатную ось, надо восстановить перпендикуляры к оси из его крайних точек. Получившийся отрезок на оси и будет ортогональной проекцией данного отрезка. Если концевые точки отрезка имели координаты (A1,B1) и (A2,B2), то его проекция на ось Ox расположится между точками (A1,0) и (A2,0). Крайними точками проекции на ось Oy станут (0,B1), (0,B2).
3. Для построения прямоугольной проекции фигуры на ось проведите перпендикуляры из крайних точек фигуры. К примеру, проекцией круга на любую ось будет отрезок, равный диаметру.
4. Чтобы получить ортогональную проекцию вектора на ось, постройте проекции начала и конца вектора. Если вектор уже перпендикулярен координатной оси, его проекция вырождается в точку. Подобно точке проецируется нулевой вектор, не имеющий длины. Если свободные векторы равны, то равны и их проекции.
5. Пусть вектор b образует с осью x угол ψ. Тогда проекция вектора на ось Пр(x)b = |b|·cosψ. Для доказательства этого положения рассмотрите два случая: когда угол ψ острый и тупой. Используйте определение косинуса, находя его отношением прилежащего катета к гипотенузе.
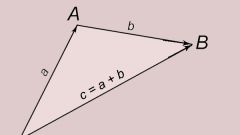
6. Рассматривая алгебраические свойства вектора и его проекций, можно заметить, что:1) Проекция суммы векторов a+b равна сумме проекций Пр(x)a+Пр(x)b;2) Проекция вектора b, умноженного на скаляр Q, равна проекции вектора b, умноженной на это же число Q: Пр(x)Qb=Q·Пр(x)b.
7. Направляющими косинусами вектора называются косинусы, образованные вектором с координатными осями Ox и Oy. Координаты единичного вектора совпадают с его направляющими косинусами. Чтобы найти координаты вектора, не равного единице, надо направляющие косинусы умножить на его длину.