Инструкция
1
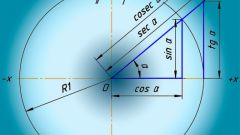
Если вам нужно посчитать угол наклона прямой к оси абсцисс, а вы не знаете уравнение прямой, опустите из любой точки этой прямой (кроме точки пересечения с осью) перпендикуляр на ось. Затем измерьте катеты полученного прямоугольного треугольника и найдите отношение прилежащего катета к противолежащему. Полученное число будет равно тангенсу угла наклона. Этот способ удобно использовать не только для изучения угла наклона прямой, но и для измерения любых углов, как на чертеже, так и в жизни (например, угол ската кровли).
2
Если вы знаете уравнение прямой, и вам нужно найти тангенс угла наклона этой прямой к оси абсцисс, выразите у через х. В результате вы получите выражение типа у=kх+b. Обратите внимание на коэффициент k – это и есть тангенс угла наклона между положительным направлением оси ох и лучом прямой, расположенным надо этой осью. Если же k=0, то тангенс также равен нулю, то есть прямая параллельна или совпадает с осью абсцисс.
3
Если вам дана сложная функция, например, квадратичная, и вам нужно найти тангенс угла наклона касательной к этой функции, или, по-другому, угловой коэффициент, вычислите производную. Затем вычислите значение производной в заданной точке, к которой будет проведена касательная. Полученное число и является тангенсом угла наклона касательной. Например, вам дана функция у=х^2+3х, посчитав ее производную, вы получите выражение у`=2х+3. Чтобы найти угловой коэффициент в точке х=3, подставьте это значение в уравнение. В результате несложных вычислений легко можно получить у=2*3+3=9, это и есть искомый тангенс.
4
Для того чтобы найти тангенс угла наклона одной из сторон треугольника к другой, поступите следующим образом. Найдите синус (sin) этого угла и разделите его на косинус (cos), в результате вы получите тангенс этого угла.