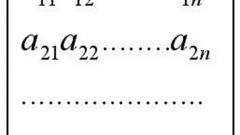Инструкция
1
Число столбцов и строк задают размерность матрицы. К примеру, таблица размерностью 5×6 имеет 5 строк и 6 столбцов. В общем случае, размерность матрицы записывается в виде m×n, где число m указывает на количество строк, n – столбцов.
2
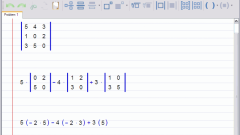
Размерность матрицы важно учитывать при совершении алгебраических операций. Например, складывать можно матрицы только одного и того же размера. Операция сложения матриц с разной размерностью не определена.
3
Если массив имеет размерность m×n, его можно умножить на массив n×l. Число столбцов первой матрицы должно равняться числу строк второй, иначе операция умножения не будет определена.
4
Размерность матрицы указывает на число уравнений в системе и количество переменных. Число строк совпадает с количеством уравнений, а за каждым столбцом закреплена своя переменная. Решение системы линейных уравнений «записано» в действиях над матрицами. Благодаря матричной системе записи становится возможным решать системы высоких порядков.
5
Если число строк равно числу столбцов, матрица называется квадратной. В ней можно выделить главную и побочную диагонали. Главная идет от левого верхнего угла к правому нижнему, побочная – от правого верхнего к левому нижнему.
6
Массивы размерностью m×1 или 1×n являются векторами. Также в виде вектора можно представить любую строку и любой столбец произвольной таблицы. Для таких матриц определены все операции над векторами.
7
Поменяв в матрице A строки и столбцы местами, можно получить транспонированную матрицу A(Т). Таким образом, при транспонировании размерность m×n перейдет в n×m.
8
В программировании для прямоугольной таблицы задается два индекса, один из которых пробегает длину всей строки, другой – длину всего столбца. При этом цикл для одного индекса помещен внутрь цикла для другого, за счет чего обеспечивается последовательное прохождение всей размерности матрицы.