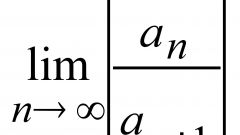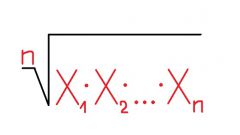Инструкция
1
Пусть есть числовая последовательность вида a_1, a_2, a_3, …, a_n и некоторая последовательность s_1, s_2, …, s_k, где n и k стремятся к ∞, а элементы последовательности s_j представляют собой суммы некоторых членов последовательности a_i. Тогда последовательность a является числовым рядом, а s - последовательностью его частичных сумм:
s_j = Σa_i, где 1 ≤ i ≤ j.
s_j = Σa_i, где 1 ≤ i ≤ j.
2
Задачи на решение числовых рядов сводятся к определению его сходимости. Говорят, что ряд сходится, если сходится последовательность его частичных сумм и абсолютно сходится, если последовательность модулей его частичных сумм сходится. И наоборот, если расходится последовательность частичных сумм ряда, то он расходится.
3
Чтобы доказать сходимость последовательности частичных сумм, необходимо перейти к понятию ее предела, который называют суммой ряда:
S = lim_n→∞ Σ_(i=1)^n a_i.
S = lim_n→∞ Σ_(i=1)^n a_i.
4
Если этот предел существует и он конечен, то ряд сходится. Если он не существует или бесконечен, то ряд расходится. Есть еще один необходимый, но не достаточный признак сходимости ряда. Это общий член ряда a_n. Если он стремится к нулю: lim a_i = 0 при I → ∞, то ряд сходится. Это условие рассматривают в совокупности с анализом других признаков, т.к. оно недостаточное, однако если общий член не стремится к нулю, то ряд однозначно расходится.
5
Пример1.
Определите сходимость ряда 1/3 + 2/5 + 3/7 + … + n/(2*n+1) + ….
Решение.
Примените необходимый признак сходимости – стремится ли общий член к нулю:
lim a_i = lim n/(2*n+1) = ½.
Итак, a_i ≠ 0, следовательно, ряд расходится.
Определите сходимость ряда 1/3 + 2/5 + 3/7 + … + n/(2*n+1) + ….
Решение.
Примените необходимый признак сходимости – стремится ли общий член к нулю:
lim a_i = lim n/(2*n+1) = ½.
Итак, a_i ≠ 0, следовательно, ряд расходится.
6
Пример2.
Определите сходимость ряда 1 + ½ + 1/3 + … + 1/n + ….
Решение.
Стремится ли общий член к нулю:
lim 1/n = 0. Да, стремится, выполнен необходимый признак сходимости, однако этого недостаточно. Теперь с помощью предела последовательности сумм попробуем доказать, что ряд расходится:
s_n = Σ_(k=1)^n 1/k = 1 + ½ + 1/3 + … + 1/n. Последовательность сумм, хоть и очень медленно, но очевидно стремится к ∞, следовательно, ряд расходится.
Определите сходимость ряда 1 + ½ + 1/3 + … + 1/n + ….
Решение.
Стремится ли общий член к нулю:
lim 1/n = 0. Да, стремится, выполнен необходимый признак сходимости, однако этого недостаточно. Теперь с помощью предела последовательности сумм попробуем доказать, что ряд расходится:
s_n = Σ_(k=1)^n 1/k = 1 + ½ + 1/3 + … + 1/n. Последовательность сумм, хоть и очень медленно, но очевидно стремится к ∞, следовательно, ряд расходится.
7
Признак сходимости Даламбера.
Пусть существует конечный предел отношения последующего и предыдущего членов ряда lim (a_(n+1)/a_n) = D. Тогда:
D 1 – ряд расходится;
D = 1 – решение неопределенно, нужно воспользоваться дополнительным признаком.
Пусть существует конечный предел отношения последующего и предыдущего членов ряда lim (a_(n+1)/a_n) = D. Тогда:
D 1 – ряд расходится;
D = 1 – решение неопределенно, нужно воспользоваться дополнительным признаком.
8
Радикальный признак сходимости Коши.
Пусть существует конечный предел вида lim √(n&a_n) = D. Тогда:
D 1 – ряд расходится;
D = 1 – нет однозначного ответа.
Пусть существует конечный предел вида lim √(n&a_n) = D. Тогда:
D 1 – ряд расходится;
D = 1 – нет однозначного ответа.
9
Эти два признака можно использовать в совокупности, однако признак Коши более сильный. Существует также интегральный признак Коши, согласно которому для определения сходимости ряда необходимо найти соответствующий определенный интеграл. Если он сходится, то сходится и ряд, и наоборот.
Видео по теме